DrawPolygonメソッドについて

お世話になっております、Yudaiと申します。

VB.NET上でPictureBoxに任意の画数の図形を描画したいのですが
座標の計算仕方が分かりません。
三角関数を使用するということは分かったのですが、教科書を見てもいまいちどう活かせば良いのか
理解できませんでした。

座標の求め方をご教示いただきたいです。　よろしくお願いいたします。

どんな図形を描きたいのでしょうか？
計算方法はものによって変わります。
台形なのか、正n角形なのか、正弦波なのかなどです。

るきお様

お返事ありがとうございます。遅くなってしまい申し訳ありません。
正n角形を描画したいです。　

Yudaiさんがどこまで理解されているのかわからないのでとりあえず簡単に一通り書きます。

正n角形はすべての頂点が同じ円周上にあります。
3角形の場合、点1と原点Oと点2が作る角度は120度です。
4角形の場合、90度です。
n角形の場合、360÷n 度 です。

つまり、１つ目の点の場所が決まれば同じ円周上の(360÷n)度先に次の点があることになります。
その次の点は(360÷n)×2度回転した先、その次の点は(360÷n)×3度回転した先にあり、この角度を利用すればすべての点の位置を決めることができます。

VBでは通常は点はxとyの座標で示すので、「回転した先」というのを (x, y)の座標で表す必要があります。

最初の１点目(点0)はたとえばy軸上にあると仮定すれば、点(0,半径) というように単純に決められます。
２つ目の点(点1)はこれを 360÷m度回転させた先にあります。

ところで、点0と原点と点1を結ぶと必ず直角三角形になります。斜辺が半径です。
xとyはそれぞれ残りの辺の長さです。
それから、この直角三角形のもう１つの角は(360÷n)度です。
以上から、この直角三角形ではすべての角の角度と斜辺の長さがわかっています。

この直角三角形の残りの2辺の長さを求めることがx,yを求めることにつながります。

さて、直角三角形の辺の長さの比率は紀元前から表にまとめられており、角度と1つの辺の長さがわかればこの比率から他の辺の長さが求められるようになっています。この比率を三角比と呼びます。三角形に辺が３つあるので、三角比には6種類あり、それぞれsin, cos, tan, cot, sec, cosecと名前がついています。

VBではMathクラスを使って角度を元にSin, Cos, Tanメソッドを使ってこの比を取得できます。
これは角度を引数にして比率を返すという観点では関数であり、三角関数と呼びます。

この理屈をプログラムしたのが下記です。
VBではy軸が学校数学と違って、下が正であることと、角度の単位がラジアンであることが大きな違いです。
このせいで学校数学では見慣れない処理が少し入りますが、理屈はここまで説明したとおりです。

※なお、ラジアンとは 360度を 2π とする単位です。180度はπです。VBではπはMath.PIで定義されています。

この例は7角形を描画します。試すにはPictureBoxを大きめに配置してください。

Private Sub PictureBox1_Paint(sender As Object, e As PaintEventArgs) Handles PictureBox1.Paint



    DrawPolygon(7, e.Graphics)



End Sub



Private Sub DrawPolygon(index As Integer, g As Graphics)



    Const radius As Integer = 200 '外接円の半径 



    '中心角(360度)をn等分したときの１角あたりの角度(単位はラジアン) 

    Dim degree As Double = (Math.PI * 2) / index



    Dim points As New List(Of Point)



    For i As Integer = 0 To index - 1



        '点0から点iの角度(角 点1-O-点iの角度)に180度加えたもの。単位はラジアン。 

        '180度 = Math.PIラジアン 

        '180度加えなくても良いのですが、学校数学とy軸の方向が逆になっているので、180度加えることで、 

        '学校数学でなじんだような配置になります。 

        Dim thisDegree As Double = degree * i + Math.PI



        '点iのx座標 

        Dim x As Double = Math.Sin(thisDegree) * radius



        '点iのy座標 

        Dim y As Double = Math.Cos(thisDegree) * radius



        'この点を記憶しておく 

        points.Add(New Point(CInt(x), CInt(y)))

    Next



    '第４象限まで見えるように平行移動させる。(既定では第１象限しか表示されていない。) 

    g.TranslateTransform(radius, radius)



    '背景色黒 

    g.Clear(Color.Black)



    '座標を配列化して間を線で結ぶ。 

    g.DrawPolygon(Pens.Blue, points.ToArray)





End Sub

正多角形は、円周を等分した点を順々に結んでできる多角形なので、

　正多角形の頂点数Ｎ(3以上)
　正多角形の外接円の中心座標Ｏ
　正多角形の第一頂点の座標Ｐ

あるいは、

　正多角形の頂点数Ｎ(3以上)
　正多角形の外接円の中心座標Ｏ
　正多角形の外接円の半径Ｒ
　正多角形の第一頂点の中心角θ

があれば求められるでしょう。（※他の方法もあります）


……などと書いているうちに、るきおさんが既に解説付きで書かれていますね。
でも折角なのでこのまま投稿。

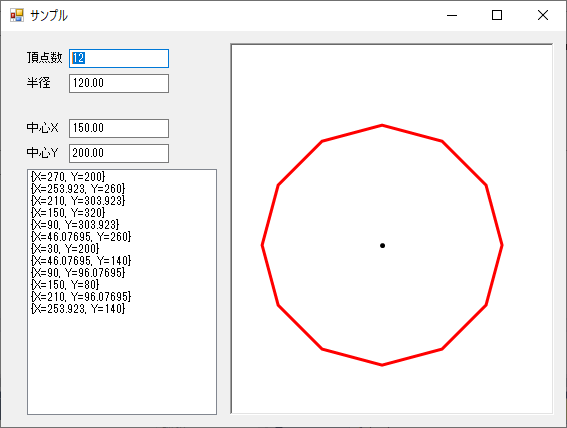
Public Class Form1



    ''' <summary>正多角形の頂点座標を取得します。</summary> 

    ''' <param name="number">頂点数</param> 

    ''' <param name="radius">半径</param> 

    ''' <param name="origin">中心座標</param> 

    ''' <param name="radian">開始角</param> 

    Public Shared Function GetRegularPolygonF(number As Integer, radius As Single, origin As PointF, Optional radian As Single = 0F) As PointF()

        If number < 3 Then

            Throw New ArgumentOutOfRangeException("number", number, "3 以上を指定してください。")

        End If

        Dim vertex(number - 1) As PointF

        Dim theta As Double = Math.PI * 2.0R / number

        For n = 0 To number - 1

            Dim d As Double = n * theta + radian

            vertex(n).X = origin.X + CSng(radius * Math.Cos(d))

            vertex(n).Y = origin.Y + CSng(radius * Math.Sin(d))

        Next

        Return vertex

    End Function



    Private number As Integer = 12

    Private radius As Single = 120.0F

    Private center As New PointF(150.0F, 200.0F)

    Private points As PointF() = {}

    Private isLoading As Boolean = True



    Private Sub Form1_Load(sender As Object, e As EventArgs) Handles MyBase.Load

        isLoading = True

        points = GetRegularPolygonF(number, radius, center)

        ListBox1.DataSource = points

        TextBox1.Text = number.ToString()

        TextBox2.Text = radius.ToString("F2")

        TextBox3.Text = center.X.ToString("F2")

        TextBox4.Text = center.Y.ToString("F2")

        isLoading = False

    End Sub



    Private Sub UpdateCoordinate()

        Try

            number = CInt(TextBox1.Text)

            radius = CSng(TextBox2.Text)

            center.X = CSng(TextBox3.Text)

            center.Y = CSng(TextBox4.Text)

            points = GetRegularPolygonF(number, radius, center)

        Catch ex As Exception

            points = New PointF() {}

            center = PointF.Empty

        End Try

    End Sub



    Private Sub TextBoxes_TextChanged(sender As Object, e As EventArgs) Handles TextBox1.TextChanged, TextBox2.TextChanged, TextBox3.TextChanged, TextBox4.TextChanged

        If isLoading Then

            Return

        End If

        UpdateCoordinate()

        ListBox1.DataSource = points

        PictureBox1.Invalidate()

    End Sub



    Private Sub PictureBox1_Paint(sender As Object, e As PaintEventArgs) Handles PictureBox1.Paint

        Try

            e.Graphics.SmoothingMode = Drawing2D.SmoothingMode.HighQuality

            e.Graphics.PixelOffsetMode = Drawing2D.PixelOffsetMode.HighQuality

            e.Graphics.Clear(Color.White)



            Using redPen As New Pen(Brushes.Red, 3)

                e.Graphics.DrawPolygon(redPen, points)  '正多角形 

            End Using



            '中心座標 

            e.Graphics.FillEllipse(Brushes.Black, center.X - 2, center.Y - 2, 5, 5)

        Catch ex As Exception

            e.Graphics.Clear(Color.Yellow)

        End Try

    End Sub

End Class

>　正多角形の頂点数Ｎ(3以上)
>　正多角形の外接円の中心座標Ｏ
>　正多角形の第一頂点の座標Ｐ
>あるいは、
>　正多角形の頂点数Ｎ(3以上)
>　正多角形の外接円の中心座標Ｏ
>　正多角形の外接円の半径Ｒ
>　正多角形の第一頂点の中心角θ

先の例は、後者のパラメータで描いたものですが、
マウスドラッグなどで描く場合は前者の方が楽かも。

Option Strict On

Imports System.Drawing.Drawing2D



Public Class Form1

  ''' <summary>正多角形の頂点座標を取得します。</summary> 

  ''' <param name="number">頂点数</param> 

  ''' <param name="origin">中心座標</param> 

  ''' <param name="point">第一頂点座標</param> 

  ''' <returns><see cref="number"/>個の要素をもつ一次元配列</returns> 

  Public Shared Function GetRegularPolygonF(number As Integer, origin As PointF, point As PointF) As PointF()

    If number < 3 Then

      Throw New ArgumentOutOfRangeException("number", number, "3 以上を指定してください。")

    End If

    Dim radian As Double = Math.Atan2(point.Y - origin.Y, point.X - origin.X)

    Dim radius As Double = (point.X - origin.X) / Math.Cos(radian)

    Dim vertex(number - 1) As PointF

    Dim theta As Double = Math.PI * 2.0R / number

    For n = 0 To number - 1

      Dim d As Double = n * theta + radian

      vertex(n).X = origin.X + CSng(radius * Math.Cos(d))

      vertex(n).Y = origin.Y + CSng(radius * Math.Sin(d))

    Next

    Return vertex

  End Function



  ''' <summary>多角形の頂点の数。NumericUpDown1 で変更する。</summary> 

  Public Property VertexCount As Integer = 7

  ''' <summary>中心座標。PictureBox1 を左クリックして指定する。</summary> 

  Public Property Origin As Nullable(Of Point)

  ''' <summary>頂点座標。PictureBox1 を左ドラッグして指定する。</summary> 

  Public Property Vertex As Point



  Private Sub Form1_Load(sender As Object, e As EventArgs) Handles MyBase.Load

    NumericUpDown1.DataBindings.Add("Value", Me, "VertexCount", False, DataSourceUpdateMode.OnPropertyChanged)

  End Sub



  Private Sub PictureBox1_Paint(sender As Object, e As PaintEventArgs) Handles PictureBox1.Paint

    If Origin IsNot Nothing Then

      Render(e.Graphics, draft:=True)

    End If

  End Sub



  Private Sub PictureBox1_MouseDown(sender As Object, e As MouseEventArgs) Handles PictureBox1.MouseDown

    If e.Button.HasFlag(MouseButtons.Left) Then

      Origin = e.Location

      Vertex = e.Location

    End If

  End Sub

  Private Sub PictureBox1_MouseMove(sender As Object, e As MouseEventArgs) Handles PictureBox1.MouseMove

    If e.Button.HasFlag(MouseButtons.Left) Then

      Vertex = e.Location

      PictureBox1.Invalidate()

    End If

  End Sub



  Private Sub PictureBox1_MouseUp(sender As Object, e As MouseEventArgs) Handles PictureBox1.MouseUp

    If Origin Is Nothing Then

      Return

    End If

    Vertex = e.Location



    '描画した多角形は累積して重ねていきたいので 

    'PictureBox に直接描画するのではなく、Image プロパティに残す 

    Dim newImage As Image

    Dim oldImage = PictureBox1.Image

    Dim rect = PictureBox1.ClientRectangle

    If oldImage Is Nothing Then

      newImage = New Bitmap(rect.Width, rect.Height)

    Else

      newImage = New Bitmap(Math.Max(oldImage.Width, rect.Width), Math.Max(oldImage.Height, rect.Height))

    End If



    Using g = Graphics.FromImage(newImage)

      g.Clear(Color.Transparent)

      If oldImage IsNot Nothing Then

        g.DrawImage(oldImage, Point.Empty)

      End If

      Render(g, draft:=False)

    End Using



    PictureBox1.Image = newImage

    Origin = Nothing



    If oldImage IsNot Nothing Then

      oldImage.Dispose()

    End If

  End Sub



  '多角形の描画 

  Private Sub Render(g As Graphics, draft As Boolean)

    Try

      Dim state = g.Save()

      g.SmoothingMode = SmoothingMode.HighQuality

      g.PixelOffsetMode = PixelOffsetMode.HighQuality



      If Origin.HasValue Then

        Using redPen As New Pen(If(draft, Brushes.Salmon, Brushes.Red), 3)

          g.DrawPolygon(redPen, GetRegularPolygonF(VertexCount, Origin.Value, Vertex))

          If draft Then

            g.FillEllipse(Brushes.Salmon, Origin.Value.X - 3, Origin.Value.Y - 3, 5, 5)

          End If

        End Using

      End If

      g.Restore(state)

    Catch ex As Exception

    End Try

  End Sub

End Class

るきお様、魔界の仮面弁士様

お返事とご教示をありがとうございます。
三角関数と言っても、教科書を見れば分かるだろうと思っていた自分が恥ずかしくなりました。
お二人の大変ご丁寧なご説明のおかげで、随分と考え方が分かりました。
お二人がお教えくださったことを参考に１度組んでみます。

結果はまたここに記します。

本当にありがとうございました。

> 三角関数と言っても、教科書を見れば分かるだろうと思っていた自分が恥ずかしくなりました。

やっていることは、それほど難しい計算ではありません。

しかしたとえ教科書レベルの理解はあったとしても、さらにそこから、
.NET に置き換えるための知識も必要になってくるとは思いますので、
画像を踏まえて、追加で解説しておきます。


まず、るきおさんが
> n角形の場合、360÷n 度 です。
と書かれていましたよね。これが一番重要な点です。

『正多角形の外接円』に対する中心角を、図で表すとこうなります。
八角形なら、360°÷8＝45°というわけですね。



中心角をθ、半径をｒ で示すと、頂点座標Ｐはこのように求められます。


あとは、『For n = 0 To (頂点数 - 1)』でループさせながら、
　「頂点座標 Ｐn の X 座標」 ＝　「半径ｒ」× Cos（ｎ×θ）
　「頂点座標 Ｐn の Ｙ 座標」 ＝　「半径ｒ」× Sin（ｎ×θ）
を求めていくだけの単純作業です。既出のサンプルコードと見比べてみてください。


一方、私が書いた
>　正多角形の頂点数Ｎ(3以上)
>　正多角形の外接円の中心座標Ｏ
>　正多角形の第一頂点の座標Ｐ
>あるいは、
>　正多角形の頂点数Ｎ(3以上)
>　正多角形の外接円の中心座標Ｏ
>　正多角形の外接円の半径Ｒ
>　正多角形の第一頂点の中心角θ
については、「前者の Ｏ と Ｐ」を後者の「Ｒ と θ」に変換しています。
そうすれば、さっきと同じループ処理によって多角形の頂点が求まります。


このパラメータ変換に使うのは、こちらの計算式。


上図において、
　ａ → 「頂点Ｐ の X 座標」
　ｂ → 「頂点Ｐ の Ｙ 座標」
　ｃ → 「半径Ｒ」
に相当します。

実際には、中心点Ｏの座標も使って、
　「水平の長さ ａ」 ＝「中心点Ｏ の X 座標」と「頂点座標 Ｐ の X 座標」の差
　「垂直の高さ ｂ」 ＝「中心点Ｏ の Ｙ 座標」と「頂点座標 Ｐ の Ｙ 座標」の差
となります。

この引き算した値を、上図公式のアークタンジェントに当てはめて中心角 θ を求めているのが、
先の私のコードでいうところのこの行にあたります。
>> Dim radian As Double = Math.Atan2(point.Y - origin.Y, point.X - origin.X)

※ Math.Atan メソッドでも求められますが、今回は Math.Atan2 メソッドを利用しました。


そして、今求めた 中心角θを使って半径 Ｒ を求める式がこちら。
やはり上の図に描かれているのと、同じ計算式ですよね。
>> Dim radius As Double = (point.X - origin.X) / Math.Cos(radian)


これにより、頂点座標 Ｐ を、半径Ｒ と 中心角θに置き換えられたので、
あとはさっきの方法と同様に For ループして、すべての頂点座標を算出したというわけです。

魔界の仮面弁士様、るきお様

遅くなってしまい、申し訳ありません。
無事解決いたしました。　今回のコードでより勉強させていただきます。
ありがとうございました。